Do you really know neural networks' optimizer?

Do you really know these optimizers in neural network training?

Vanilla SGD

$x_{t+1} = x_t - \alpha \nabla f(x_t)$

dx = compute_gradient(x)
x += learning_rate * dx

SGD + Momentum

$v_{t+1} = \rho v_t + \nabla f(x_t)$

$x_{t+1} = x_t - \alpha v_{t+1}$

1. Build up “velocity” as a running mean of gradients
2. Rho gives “friction”; typically rho=0.9 or 0.99

dx = compute_gradient(x)
vx = rho * vx + dx
x += learning_rate * vx

Nesterov Momentum

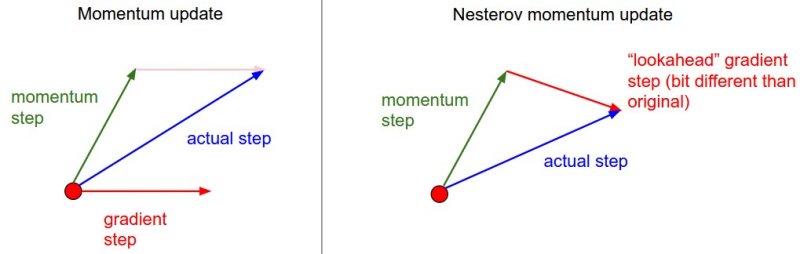
Momentum update is like a correction of gradient step based on previous route. Nesterov Momentum is a gradient step after taking momentum step. Both methods consist of 2 components: a big jump based on accumulated gradient (momentum) and a small jump based on the gradient at a new location. The difference is in what order these two steps are taken in. Standard momentum uses gradient at current location and then takes a big jump in direction of momentum. Nesterov takes a big jump based on accumulated gradient then makes a small corrective jump based on gradient.

x_ahead = x + mu * v
# evaluate dx_ahead (the gradient at x_ahead instead of at x)
v = mu * v - learning_rate * dx_ahead
x += v

or

v_prev = v # back this up
v = mu * v - learning_rate * dx # velocity update stays the same
x += -mu * v_prev + (1 + mu) * v # position update changes form

AdaGrad

dx = compute_gradient(x)
grad_squared += dx * dx
x -= learning_rate * dx / (np.sqrt(grad_squared) + 1e-7)

Notice that the weights that receive high gradients will have their effective learning rate reduced, while weights that receive small or infrequent updates will have their effective learning rate increased.
A downside of Adagrad is that in case of Deep Learning, the monotonic learning rate usually proves too aggressive and stops learning too early.

RMSProp

dx = compute_gradient(x)
grad_squared = decay_rate * grad_squared + (1 - decay_rate) *dx * dx
x -= learning_rate * dx / (np.sqrt(grad_squared) + 1e-7)

The RMSProp update adjusts the Adagrad method in a very simple way in an attempt to reduce its aggressive, monotonically decreasing learning rate.

Adam

Sort of like RMSProp with momentum

dx = compute_gradient(x)
first_moment = beta1 * first_moment + (1 - beta1) * dx # Mmentum
second_moment = beta2 * second_moment + (1 - beta2) *dx *dx
first_unbias = first_moment / (1 - beta1 ** iter) # Bias correction
second_unbias = second_moment / (1 - beta2 ** t)
x -= learning_rate * first_unbias / (np.sqrt(second_unbias) + 1e-7) # AdaGrad/RMSProp

Adam with beta1 = 0.9, beta2 = 0.999, and learning_rate = 1e-3 or 5e-4 is a great starting point for many models.

Two great gif that explains everything!

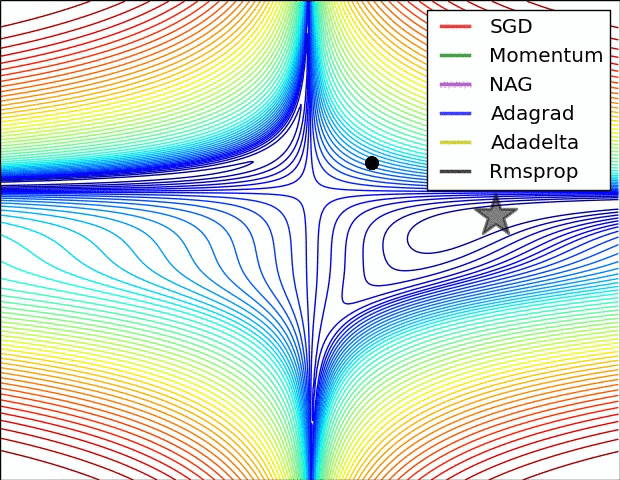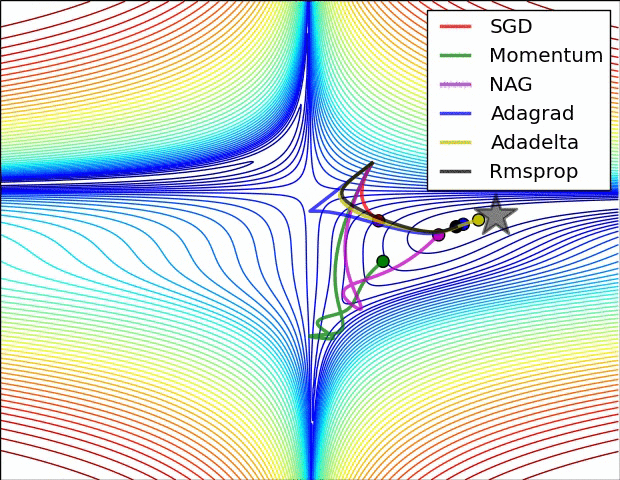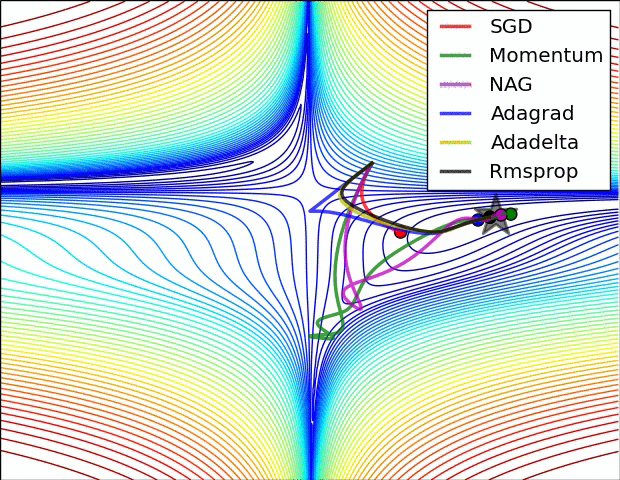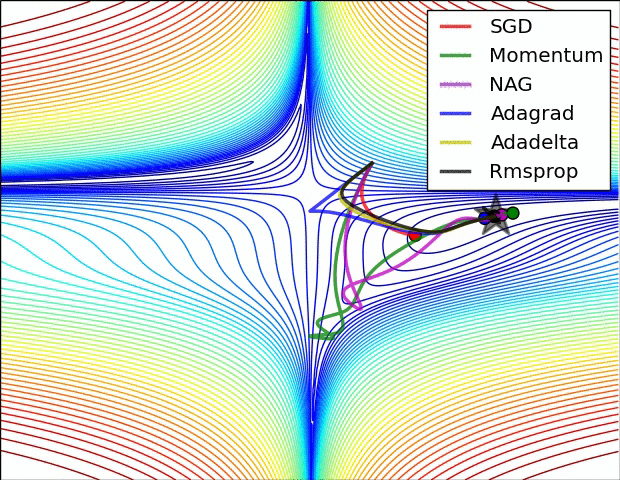
Contours of a loss surface and time evolution of different optimization algorithms. Notice the “overshooting” behavior of momentum-based methods, which make the optimization look like a ball rolling down the hill.

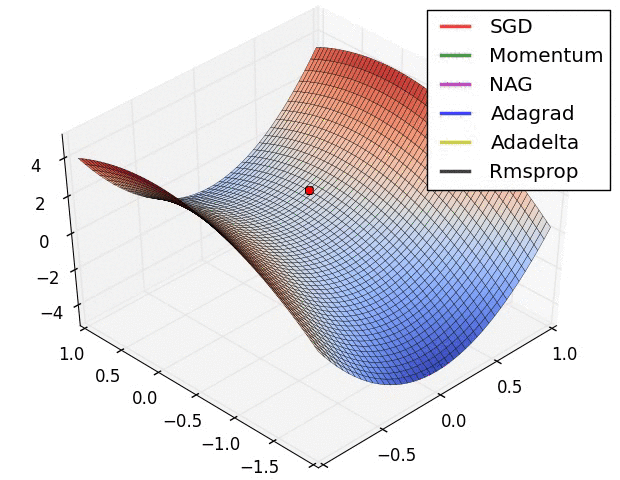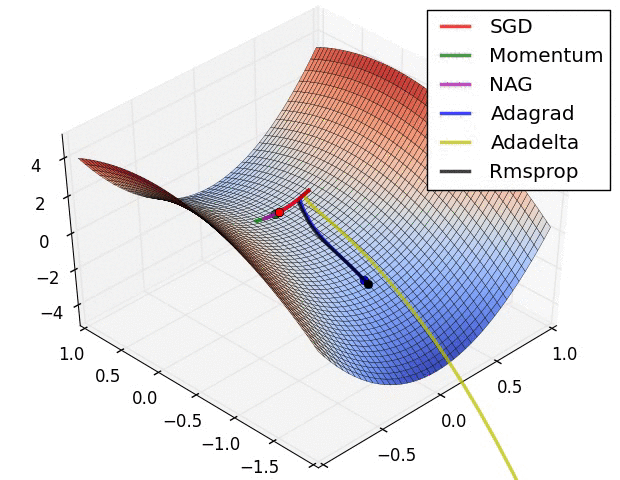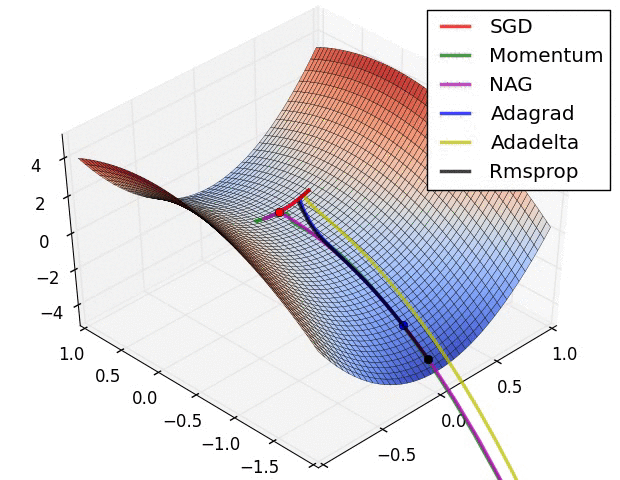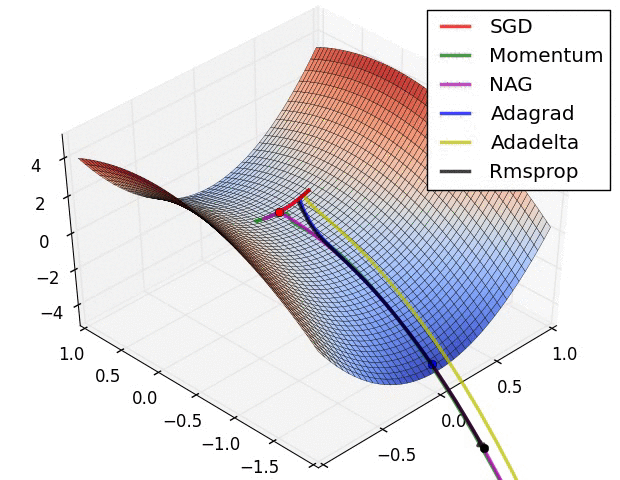
A visualization of a saddle point in the optimization landscape, where the curvature along different dimension has different signs (one dimension curves up and another down). Notice that SGD has a very hard time breaking symmetry and gets stuck on the top. Conversely, algorithms such as RMSprop will see very low gradients in the saddle direction. Due to the denominator term in the RMSprop update, this will increase the effective learning rate along this direction, helping RMSProp proceed.
Images credit: Alec Radford.

Summary

The two recommended updates to use are either SGD+Nesterov Momentum or Adam.

Usually, SGD takes more time for training and is prone to be trapped in a saddle point. With a good initialization and learning rate strategy, the result can be more reliable. If you want a faster converge, adaptive learning rate methods are recommended.